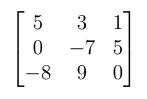Chapitre 1 Déterminant d'une matrice
À en croire cette page Wikipédia, le Japonais Seki Kowa fut le premier à introduire des déterminants de taille 3 et 4. 
Plus récemment, l'Anglais Tim Gowers a enregistré ses réflexions sur le déterminant des matrices de Pascal symétriques dans une série de trois vidéos dont voici la dernière :
Section 1.1 Théorie
Proposition 1.1.1.
Quelle que soit la façon dont on définisse le déterminant d'une matrice carrée, on a
Définition 1.1.2.
Une matrice carrée \(A\) de taille \(n\times n\) est dite inversible s'il existe une matrice carrée \(B\) de même taille telle que
Théorème 1.1.3.
Une matrice carrée est inversible si et seulement si son déterminant n'est pas nul.
Démonstration.
Soit \(A\) une matrice \(n\times n\) inversible et \(B\) sa matrice inverse, de sorte que
Raisonnons par l'absurde et supposons que \(\det(A)\) soit nul. On a alors
Il découle de cette contradiction que le nombre \(\det(A)\) n'est pas nul.
Je vous laisse le soin de démontrer la réciproque.
Section 1.2 Calcul
Voici comment calculer le déterminant de la matrice
à l'aide de la fonction det du module linalg de NumPy :
Et voilà comment faire la même chose avec Sage :
Le code suivant vous permet de vérifier une propriété du déterminant. Laquelle ?
Section 1.3 Exercices
Exercice 1.3.1.
On s'intéresse à la matrice
- Calculez le déterminant de \(A\text{.}\)
- Déduisez-en le déterminant de \(A^5\text{.}\)
- \(-2\text{.}\)
- \(-32\text{.}\)
- Grâce à la règle de calcul d'un déterminant \(2\times 2\text{,}\) on a\begin{equation*} \det(A)=1\times 4-2\times 3=-2. \end{equation*}
- Par multiplicativité du déterminant, on a\begin{equation*} \det(A^5)=\left(\det(A)\right)^5=(-2)^5=-32. \end{equation*}
Exercice 1.3.2.
Utilisez Desmos pour illustrer le déterminant de deux vecteurs.
Je préfère cette application GeoGebra de Brian Sterr.