Sauter

Section 3.8 Calculs de longueurs, d'aires et de volumes

Déterminez la longueur de la courbe donnée.

  1. \(\displaystyle y=\frac{x^3}{3}+\frac{1}{4x}\) pour \(1\leq x\leq 2\)

  2. \(\displaystyle x=\frac{\sqrt{y}(y-3)}{3}\) pour \(1\leq y\leq 9\)

Réponse

  1. \(\displaystyle\frac{59}{3}\)

  2. \(\displaystyle\frac{32}{3}\)

Déterminez l'aire de la surface fermée comprise entre l'axe des abscisses et le graphique de la fonction \(f(x)=x^3-x^2-2x\text{.}\)

Réponse

\(\displaystyle\frac{37}{12}\)

Déterminez l'aire de la surface fermée comprise entre l'axe des ordonnées et le graphique de la courbe \(\frac{x}{3}=1-y^4\text{.}\)

Réponse

\(\displaystyle\frac{24}{5}\)

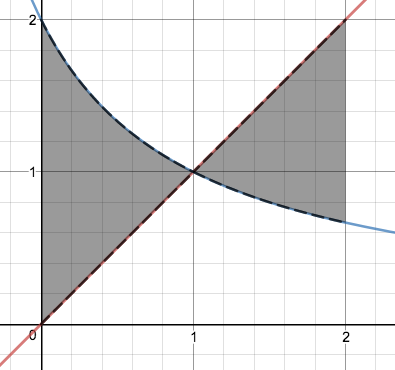
Sachant que les courbes ci-dessous correspondent aux équations \(\displaystyle y=x\) et \(\displaystyle y=\frac{2}{x+1}\text{,}\) calculez l'aire des régions ombrées.

1.

2.

Réponse

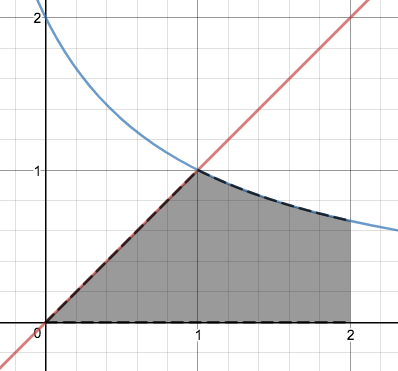
  1. \(\displaystyle\frac{1}{2}+2\ln\left(\frac{3}{2}\right)\)

  2. \(\displaystyle 1+4\ln(2)-2\ln(3)\)

Calculez l'aire des régions fermées comprises entre les courbes indiquées.

  1. \(\displaystyle y=x\) et \(\displaystyle y=x^3\)

  2. \(\displaystyle x=y^2\) et \(\displaystyle x=5y-6\)

  3. \(\displaystyle y=2x^2-5\) et \(\displaystyle y=7-x^2\)

  4. \(\displaystyle y^2=x+1\) et \(\displaystyle y=x-1\)

Réponse

  1. \(\displaystyle \frac{1}{2}\)

  2. \(\displaystyle \frac{1}{6}\)

  3. \(\displaystyle 32\)

  4. \(\displaystyle \frac{9}{2}\)

Déterminez l'aire de la région sous la courbe d'équation \(\displaystyle y=\frac{1}{x^3}\)

  1. entre \(x=1\) et \(x=10\)

  2. entre \(x=1\) et \(x=100\)

  3. pour \(x\geq 1\)

Réponse

  1. \(\displaystyle\frac{99}{200}\)

  2. \(\displaystyle\frac{9999}{20000}\)

  3. \(\displaystyle\frac{1}{2}\)

Évaluez l'aire de la surface obtenue par rotation de la courbe donnée autour de l'axe indiqué.

  1. courbe: \(\displaystyle y=\sqrt{4-x^2}\) pour \(-1\leq x\leq 1\) - axe: \(y=0\)

  2. courbe: \(\displaystyle x=1+2y^2\) pour \(1\leq y\leq 2\) - axe: l'axe des \(x\)

  3. courbe: \(\displaystyle y=x^2\) pour \(1\leq x\leq 2\) - axe: \(x=0\)

Réponse

  1. \(\displaystyle 8\pi\)

  2. \(\displaystyle\frac{\pi}{24}\left(65\sqrt{65}-17\sqrt{17}\right)\)

  3. \(\displaystyle\frac{\pi}{6}\left(17\sqrt{17}-5\sqrt{5}\right)\)

Calculez le volume du solide obtenu par rotation autour de l'axe indiqué de la région fermée délimitée par les courbes données. Utilisez la méthode de votre choix.

  1. région: \(\displaystyle y=2-\frac{x}{2}\;;\;y=0\;;\;x=1\;;\;x=2\) - axe: l'axe des \(x\)

  2. région: \(\displaystyle y=x\;;\;y=x^2\) - axe: \(y=0\)

  3. région: \(\displaystyle y=2x^2-x^3\;;\;y=0\) - axe: l'axe des \(y\)

  4. région: \(\displaystyle y=x-x^2\;;\;y=0\) - axe: \(x=2\)

  5. région: \(\displaystyle y=x^2\;;\;x=y^2\) - axe: \(y=1\)

  6. région: \(\displaystyle x=y^3\;;\;y=0\;;\;x=1\) - axe: \(x=2\)

Réponse

  1. \(\displaystyle\frac{19\pi}{12}\)

  2. \(\displaystyle\frac{2\pi}{15}\)

  3. \(\displaystyle\frac{16\pi}{5}\)

  4. \(\displaystyle\frac{\pi}{2}\)

  5. \(\displaystyle\frac{11\pi}{30}\)

  6. \(\displaystyle\frac{3\pi}{5}\)

Calculez le volume du solide obtenu par rotation de la surface délimitée par \(f(x)=x^2\) et \(g(x)=4\) pour \(x\geq 0\)

  1. autour de l'axe des abscisses.

  2. autour de l'axe des ordonnées.

  3. autour de l'axe \(y=5\text{.}\)

  4. autour de l'axe \(x=3\text{.}\)

Réponse

  1. \(\displaystyle\frac{128\pi}{5}\)

  2. \(\displaystyle 8\pi\)

  3. \(\displaystyle\frac{416\pi}{15}\)

  4. \(\displaystyle 24\pi\)