Section 2.2 Tangentes
¶Exercice 2.2.1.
Déterminez la pente de la tangente à la courbe donnée par l'équation \(\displaystyle e^x\ln(y)=2xy\) au point \(\displaystyle (0\,;\,1)\text{.}\)
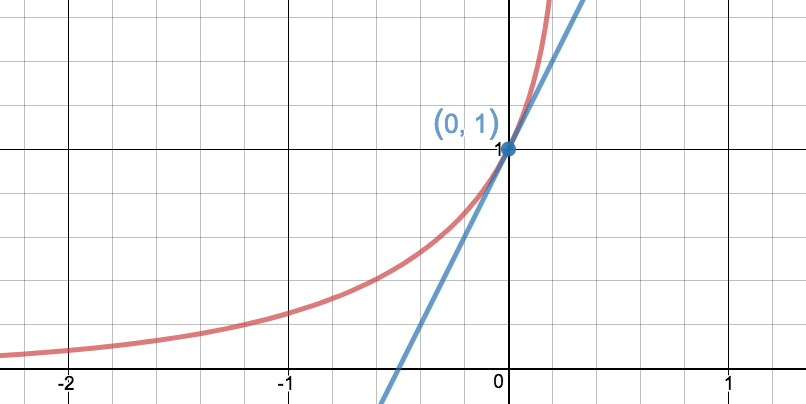
Réponse
\(\displaystyle 2\)
Exercice 2.2.2.
Déterminez l'équation de la tangente à la courbe donnée par l'équation \(\displaystyle y=\ln\left(e^x-1\right)\) au point \(\displaystyle (\ln(2)\,;\,0)\text{.}\)
Réponse
\(y=2x-2\ln(2)\)
Exercice 2.2.3.
Déterminez l'équation de chacune des tangentes à la courbe donnée par l'équation \(\displaystyle x^2-xy+y^2=x-y\) lorsque \(\displaystyle x=0\text{.}\)
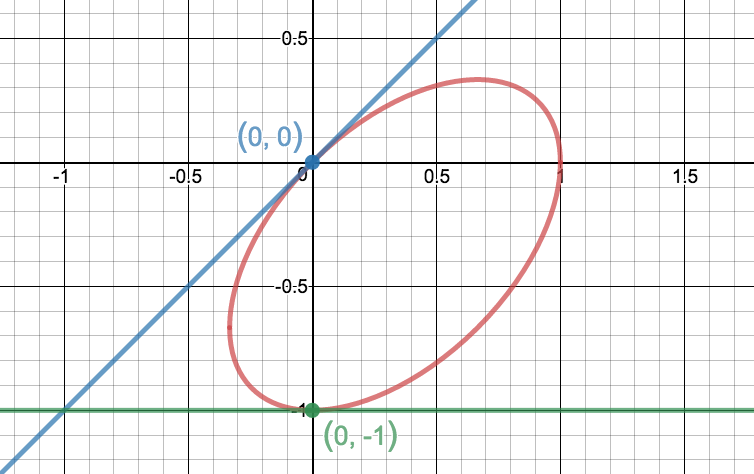
Réponse
\(\displaystyle y=x\) au point \(\displaystyle (0\,;\,0)\) et \(\displaystyle y=-1\) au point \(\displaystyle (0\,;\,-1)\)
