Section 2.4 Étude de fonctions
¶Exercice 2.4.1.
Déterminez les extremums absolus de la fonction \(\displaystyle f(x)=x-2\arctan(x)\) sur l'intervalle \(\displaystyle [0\,;\,4]\text{.}\)
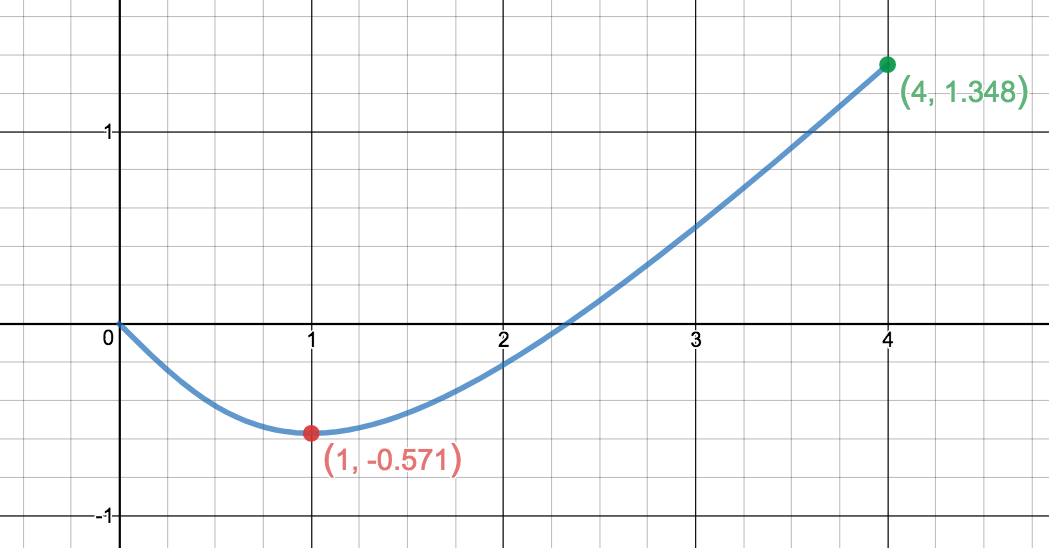
\(\displaystyle f(1)=1-\frac{\pi}{2}\approx -0,57\) est le minimum absolu et \(\displaystyle f(4)=4-2\arctan(4)\approx 1,35\) le maximum absolu.
Exercice 2.4.2.
Déterminez les extremums absolus de la fonction \(\displaystyle f(x)=\frac{2-x}{5+x^2}\) sur \(\displaystyle \mathbb{R}\text{.}\)
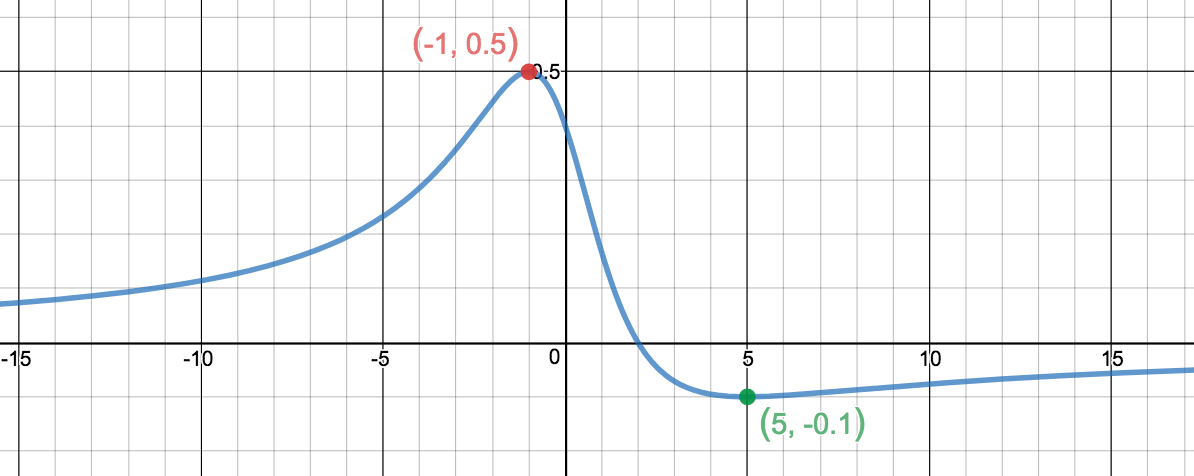
\(\displaystyle f(5)=-0,1\) est le minimum absolu et \(\displaystyle f(-1)=0,5\) le maximum absolu.
Exercice 2.4.3.
Déterminez les intervalles de concavité et les points d'inflexion de la fonction \(\displaystyle f(x)=3+\cos(x)\) sur l'intervalle \(\displaystyle [-\pi/2\,;\,\pi]\text{.}\)
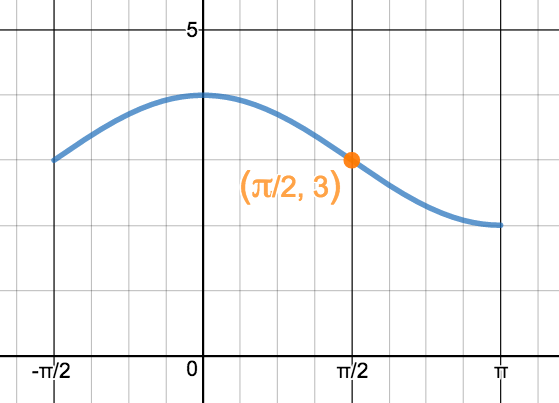
La fonction est concave vers le bas sur \(\displaystyle [-\pi/2\,;\,\pi/2]\text{,}\) concave vers le haut sur \(\displaystyle [\pi/2\,;\,\pi]\text{.}\)
Elle admet un point d'inflexion en \(\displaystyle (\pi/2\,;\,3)\)
.Exercice 2.4.4.
Déterminez les intervalles de concavité et les points d'inflexion de la fonction \(\displaystyle f(x)=\ln^2x\) sur \(\displaystyle ]0\,;\,+\infty[\text{.}\)
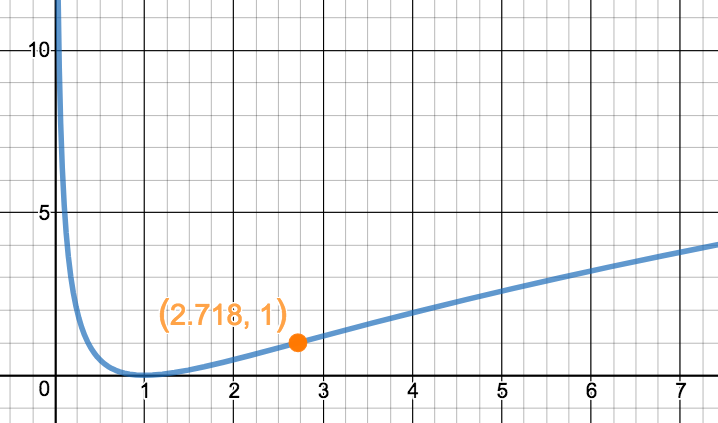
La fonction est concave vers le haut sur \(\displaystyle ]0\,;\,e[\text{,}\) concave vers le bas sur \(\displaystyle [e\,;\,+\infty[\text{.}\)
Elle admet un point d'inflexion en \(\displaystyle (e,;\,1)\)
.Exercice 2.4.5.
Faites l'étude complète de la fonction \(\displaystyle f(x)=\frac{x^3}{x-3}\) et esquissez sa représentation graphique.
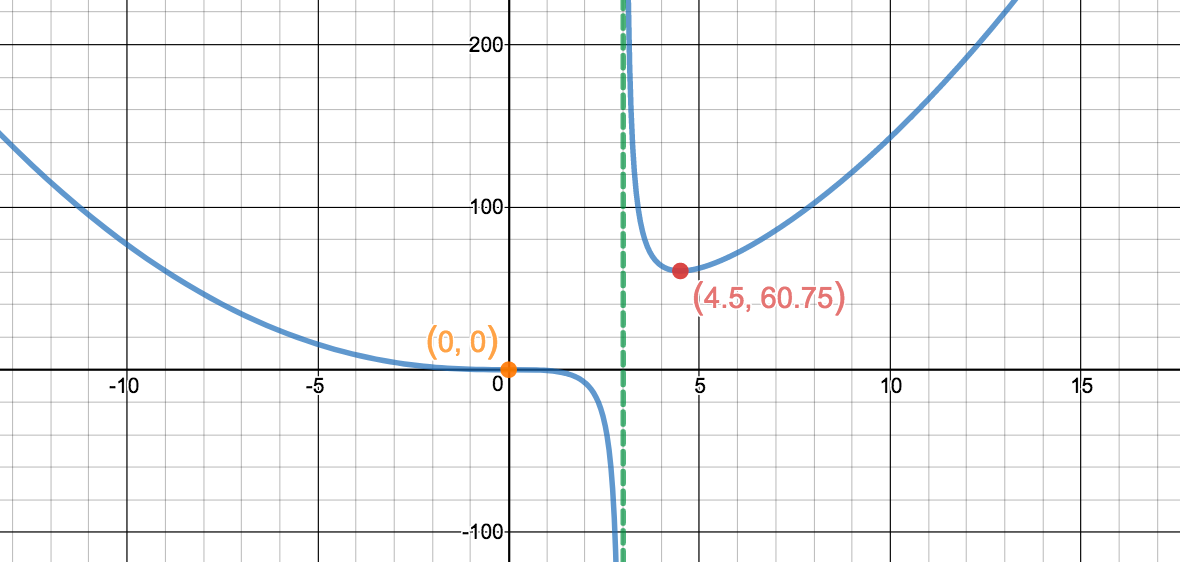
Le domaine de la fonction est \(\displaystyle \mathbb{R}\setminus\{3\}\text{.}\)
Elle est décroissante sur \(\displaystyle ]-\infty\,;\,3[\cup]3\,;\,4,5]\text{,}\) décroissante sur \(\displaystyle [4,5\,;\,+\infty[\text{.}\)
Elle est concave vers le haut sur \(\displaystyle ]-\infty\,;\,0]\cup]3\,;\,+\infty[]\text{,}\) concave vers le bas sur \(\displaystyle [0\,;\,3[\text{.}\)
Elle admet un minimum relatif en \(\displaystyle (4,5\,;\,60,75)\) et un point d'inflexion en \(\displaystyle (0,;\,0)\text{.}\)
La droite \(\displaystyle x=3\) est une asymptote verticale.
