M&A Exercices

Section 2.3 Exercices

Exercice 2.3.1.

Codez une fonction pairOuImpair(n) qui renvoie \(\text{pair}\) si \(\text{n}\) est divisible par \(2\text{,}\) et \(\text{impair}\) si ce n'est pas le cas.

Testez votre code avec print(pairOuImpair(347)) et print(pairOuImpair(504)) qui doivent afficher \(\text{impair}\) et \(\text{pair}\) respectivement.

Indication

Vous pourriez avoir besoin de l'opérateur modulo %.

Solution

def pairOuImpair(n):
    if n % 2 == 0:
        return 'pair'
    else:
        return 'impair'

print(pairOuImpair(347))
print(pairOuImpair(504))

Exercice 2.3.2.

Codez une fonction aireTrapeze(base1, base2, hauteur) qui renvoie l'aire d'un trapèze en fonction des longueurs de ses deux bases et de sa hauteur.

Testez votre code avec print(aireTrapeze(4, 7, 3) qui doit afficher \(\text{16.5}\text{.}\)

Solution

def aireTrapeze(base1, base2, hauteur):
    return (base1 + base2) * hauteur * 0.5

print(aireTrapeze(4, 7, 3))

Exercice 2.3.3.

Codez la fonction f(x) définie par

\begin{equation*} f(x)= \begin{cases} 3&\text{si}&x\le -2,\\ x^2+3&\text{si}&-2<x<5,\\ 4-5x&\text{si}&x\ge 5. \end{cases} \end{equation*}

Testez votre code avec les cas suivants.

print(f(-4)) doit afficher \(\text{3}\text{.}\)
print(f(2)) doit afficher \(\text{7}\text{.}\)
print(f(5)) doit afficher \(\text{-21}\text{.}\)

Solution

def f(x):
    if x <= - 2:
        return 3
    elif x < 5:
        return x ** 2 + 3
    else:
        return 4 - 5 * x

print(f(-4))
print(f(2))
print(f(5))

Exercice 2.3.4.

Codez la fonction f(x) correspondant au graphique qui suit.

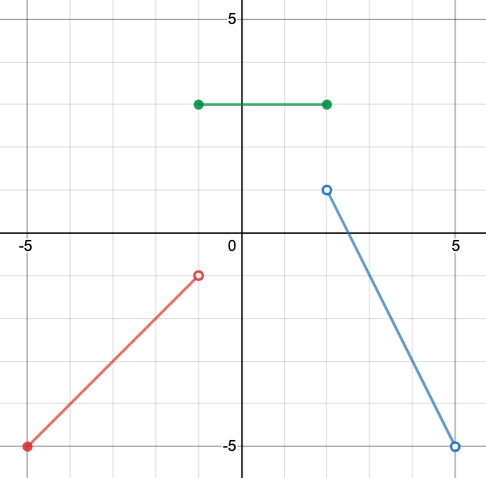
Testez votre code avec les cas suivants.

print(f(-7)) doit afficher \(\text{non défini}\text{.}\)
print(f(-5)) doit afficher \(\text{-5}\text{.}\)
print(f(-1)) doit afficher \(\text{3}\text{.}\)
print(f(2.5)) doit afficher \(\text{0.0}\text{.}\)
print(f(5)) doit afficher \(\text{non défini}\text{.}\)

Solution

def f(x):
    if x < -5:
        return 'non défini'
    elif x < -1:
        return x
    elif x <= 2:
        return 3
    elif x < 5:
        return - 2 * x + 5
    else:
        return 'non défini'

print(f(-7))
print(f(-5))
print(f(-1))
print(f(2.5))
print(f(5))

Exercice 2.3.5.

À l'aide d'une boucle for, construisez une fonction sommeEntiers(n) qui renvoie la somme des entiers de \(\text{1}\) jusqu'à \(\text{n}\text{.}\)

Testez votre code avec print(sommeEntiers(1000)) qui doit afficher \(\text{500500}\text{.}\)

Solution

def sommeEntiers(n):
    somme = 1
    for k in range(2, n+1):
        somme = somme + k
    return somme

print(sommeEntiers(1000))

Exercice 2.3.6.

Créez une fonction conversion(mesure, echelle) qui convertit

mesure en Fahrenheit si echelle vaut 'C';
mesure en Celsius si echelle vaut 'F'.

Testez votre code avec les cas suivants.

print(conversion(17, 'C')) doit afficher \(\text{62.6}\text{.}\)
print(conversion(84, 'F')) doit afficher \(\text{28.8888888889}\text{.}\)

Solution

def conversion(mesure, echelle):
    if echelle == 'C':
        return mesure * 1.8 + 32
    elif echelle == 'F':
        return (mesure - 32.0) * 5 / 9

print(conversion(17, 'C'))
print(conversion(84, 'F'))

Exercice 2.3.7.

Créez une fonction natureTriangle(a, b, c) qui renvoie

\(\text{impossible}\text{,}\)
\(\text{équilatéral}\text{,}\)
\(\text{isocèle}\text{,}\)
ou \(\text{scalène}\)

selon les valeurs des longueurs des côtés \(\text{a, b, c}\) d'un triangle.

Testez votre code avec les cas suivants.

print(natureTriangle(1, 2, 4)) doit afficher \(\text{impossible}\text{.}\)
print(natureTriangle(2, 2, 2)) doit afficher \(\text{équilatéral}\text{.}\)
print(natureTriangle(2, 2, 3)) doit afficher \(\text{isocèle}\text{.}\)
print(natureTriangle(1, 2, 2.5)) doit afficher \(\text{scalène}\text{.}\)

Solution

def natureTriangle(a, b, c):
    if (a > b + c) or (b > a + c) or (c > a + b):
        return 'impossible'
    elif (a == b) and (a == c):
        return 'équilatéral'
    elif (a == b) or (a == c) or (b == c):
        return 'isocèle'
    else:
        return 'scalène'

print(natureTriangle(1, 2, 4))
print(natureTriangle(2, 2, 2))
print(natureTriangle(2, 2, 3))
print(natureTriangle(1, 2, 2.5))

Exercice 2.3.8.

Soit \([a;b]\) un intervalle et \(n\geq 1\) un entier.

On appelle subdivision régulière de \([a;b]\) en \(n\) sous-intervalles de longueur

\begin{equation*} \Delta x:=\frac{b-a}{n} \end{equation*}

la suite

\begin{equation*} a=x_0<x_1<x_2<\cdots<x_{n-1}<x_n=b \end{equation*}

où

\begin{equation*} x_k-x_{k-1}=\Delta x\qquad\text{pour tout}\;k=1,\ldots,n. \end{equation*}

Par exemple, voici la subdivision régulière de \([1;3]\) en quatre sous-intervalles de même longueur :

\begin{equation*} x_0=1\;< x_1=1{,}5\;< x_2=2\;< x_3=2{,}5\;< x_4=3. \end{equation*}

À l'aide d'une boucle for, codez une fonction subdivisionReguliere1(a, b, n) qui affiche \(x_k\) pour \(k=0,1,\ldots,n\) sans rien renvoyer.

Testez votre code avec subdivisionReguliere1(1.0, 3.0, 4) qui doit afficher
```
1.0
1.5
2.0
2.5
3.0
```
À l'aide d'une boucle while, codez une fonction subdivisionReguliere2(a, b, n) qui renvoie la liste \(\left[x_0,x_1,\ldots,x_n\right]\text{.}\)

Testez votre code avec print(subdivisionReguliere2(1.0, 3.0, 4)) qui doit afficher
```
[1.0, 1.5, 2.0, 2.5, 3.0]
```

Solution 1

def subdivisionReguliere1(a, b, n):
    deltaX = (b - a) / n
    x = a
    print(x)
    for k in range(0, n):
        x = x + deltaX
        print(x)

subdivisionReguliere1(1.0, 3.0, 4)

def subdivisionReguliere2(a, b, n):
    deltaX = (b - a) / n
    x = a
    liste = [a]
    while x < b:
        x = x + deltaX
        liste.append(x)
    return liste

print(subdivisionReguliere2(1.0, 3.0, 4))

Solution 2

def subdivisionReguliere1(a, b, n):
    deltaX = (b - a) / n
    x = a
    for k in range(0, n+1):
        print(x)
        x = x + deltaX

subdivisionReguliere1(1.0, 3.0, 4)

def subdivisionReguliere2(a, b, n):
    deltaX = (b - a) / n
    liste = []
    x = a
    while x <= b:
        liste.append(x)
        x = x + deltaX
    return liste

print(subdivisionReguliere2(1.0, 3.0, 4))

Exercice 2.3.9.

Codez une fonction sommeEntiers(n) qui renvoie la somme des entiers de \(\text{1}\) à \(\text{n}\) de manière récursive.

Testez votre code avec les cas suivants.

print(sommeEntiers(3)) doit afficher \(\text{6}\text{.}\)
print(sommeEntiers(100)) doit afficher \(\text{5050}\text{.}\)

Indication

\begin{equation*} \sum_{k=1}^nk=\underbrace{1+2+\cdots+(n-1)}_{\displaystyle\sum_{k=1}^{n-1}k}+n \end{equation*}

Solution

def sommeEntiers(n):
    if n == 1:
        return 1
    else:
        return n + sommeEntiers(n - 1)

print(sommeEntiers(3))
print(sommeEntiers(100))

Exercice 2.3.10.

On appelle suite de Syracuse toute suite d'entiers naturels \(\{s_n\}\) définie par la donnée d'un entier de départ \(s_0\geq 1\) et la relation de récurrence qui suit.

\begin{equation*} \quad s_{n+1} = \begin{cases} s_n/2&\text{si}\;s_n\;\text{est pair,}\\ 3s_n+1&\text{sinon,} \end{cases} \quad\text{pour tout}\;n\geq 0. \end{equation*}

Codez une fonction syracuse1(s, n) qui renvoie, à l'aide d'une boucle for, le terme \(s_{\text{n}}\) d'une suite de Syracuse commençant par \(s_0=\text{s}\text{.}\)
Codez une fonction syracuse2(s, n) qui renvoie, de manière récursive, le terme \(s_{\text{n}}\) d'une suite de Syracuse commençant par \(s_0=\text{s}\text{.}\)

Testez votre code avec print(syracusej(14, 20)) qui doit afficher \(\text{1}\text{.}\)

Solution

def syracuse1(s, n):
    for k in range(1, n+1):
        if s % 2 == 0:
              s = s / 2
        else:
            s = 3 * s + 1
    return s

print(syracuse1(14, 20))

def syracuse2(s, n):
    if n == 0:
        return s
    elif s % 2 == 0:
        return syracuse2(s / 2, n-1)
    else:
        return syracuse2(3 * s + 1, n-1)

print(syracuse2(14, 20))

Exercice 2.3.11.

Combien de fois le nombre \(45\) est-il divisible par \(2\text{?}\) La réponse est \(0\) car \(45\) n'est pas divisible par \(2\text{.}\)

Combien de fois le nombre \(24\) est-il divisible par \(2\text{?}\) La réponse est \(3\) car \(24=2^3\cdot 3\) est divisible par \(2^3\text{,}\) mais \(24/2^3=3\) n'est pas divisible par \(2\text{.}\)

En utilisant une variable compteur et une boucle while, codez une fonction combienDeDeux1(n) qui renvoie le nombre de fois que \(\text{n}\) est divisible par \(2\text{.}\)
Codez une fonction combienDeDeux2(n) qui renvoie, de manière récursive, le nombre de fois que \(\text{n}\) est divisible par \(2\text{.}\)

Testez votre code avec combienDeDeuxj(45) et combienDeDeuxj(24) qui doivent afficher \(\text{0}\) et \(\text{3}\) respectivement.

Indication

Dans \(24\text{,}\) il y a un facteur \(2\) de plus que dans \(24/2=12\text{.}\)
Dans \(12\text{,}\) il y a un facteur \(2\) de plus que dans \(12/2=6\text{.}\)
Dans \(6\text{,}\) il y a un facteur \(2\) de plus que dans \(6/2=3\text{.}\)
Dans \(3\text{,}\) il n'y a aucun facteur égal à \(2\text{.}\)

Solution

def combienDeDeux1(n):
    compteur = 0
    while n % 2 == 0:
        compteur = compteur + 1
        n = n / 2
    return compteur

print(combienDeDeux1(45))
print(combienDeDeux1(24))

def combienDeDeux2(n):
    if n % 2 != 0:
        return 0
    else:
        return 1 + combienDeDeux2(n / 2)

print(combienDeDeux2(45))
print(combienDeDeux2(24))

Exercice 2.3.12.

La suite de Fibonacci est définie par récurrence de la façon suivante :

\begin{equation*} F_1=F_2=1\quad\text{et}\quad F_n=F_{n-1}+F_{n-2}\;\text{pour tout}\;n\geq 3. \end{equation*}

Calculez \(F_{20}\) à l'aide d'une fonction récursive.
Pouvez-vous calculer \(F_{100}\) de cette façon?

Solution

On obtient

\begin{equation*} F_{20}=6765 \end{equation*}

à l'aide du code qui suit.

def fibonacci(n):
    if n == 1:
        return 1
    elif n == 2:
        return 1
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

print(fibonacci(20))

Non, cela prend trop de temps. Il vaut mieux s'en tenir à la méthode de l'exercice 1.4.12.