Avancer

Section 4.1 Les dérivées partielles

Outils 4.1.1.

  • Calculatrice à dérivées partielles :

  • Application GeoGebra illustrant graphiquement le concept de dérivée partielle.

  • Exemple de calcul de dérivée partielle avec WolframAlpha.

Soit S la surface d'équation

\begin{equation*} z=x^2+y^2. \end{equation*}

  1. Calculez la pente de la tangente à la trace de la surface S dans le plan d'équation

    \begin{equation*} y=2 \end{equation*}

    au point \((1,2,5)\text{.}\)

  2. Calculez la pente de la tangente à la trace de la surface S dans le plan d'équation

    \begin{equation*} x=1 \end{equation*}

    au point \((1,2,5)\text{.}\)

Indication

Pour commencer, utilisez votre logiciel préféré pour interpréter graphiquement la question. Voici à quoi ressemble la surface en rouge

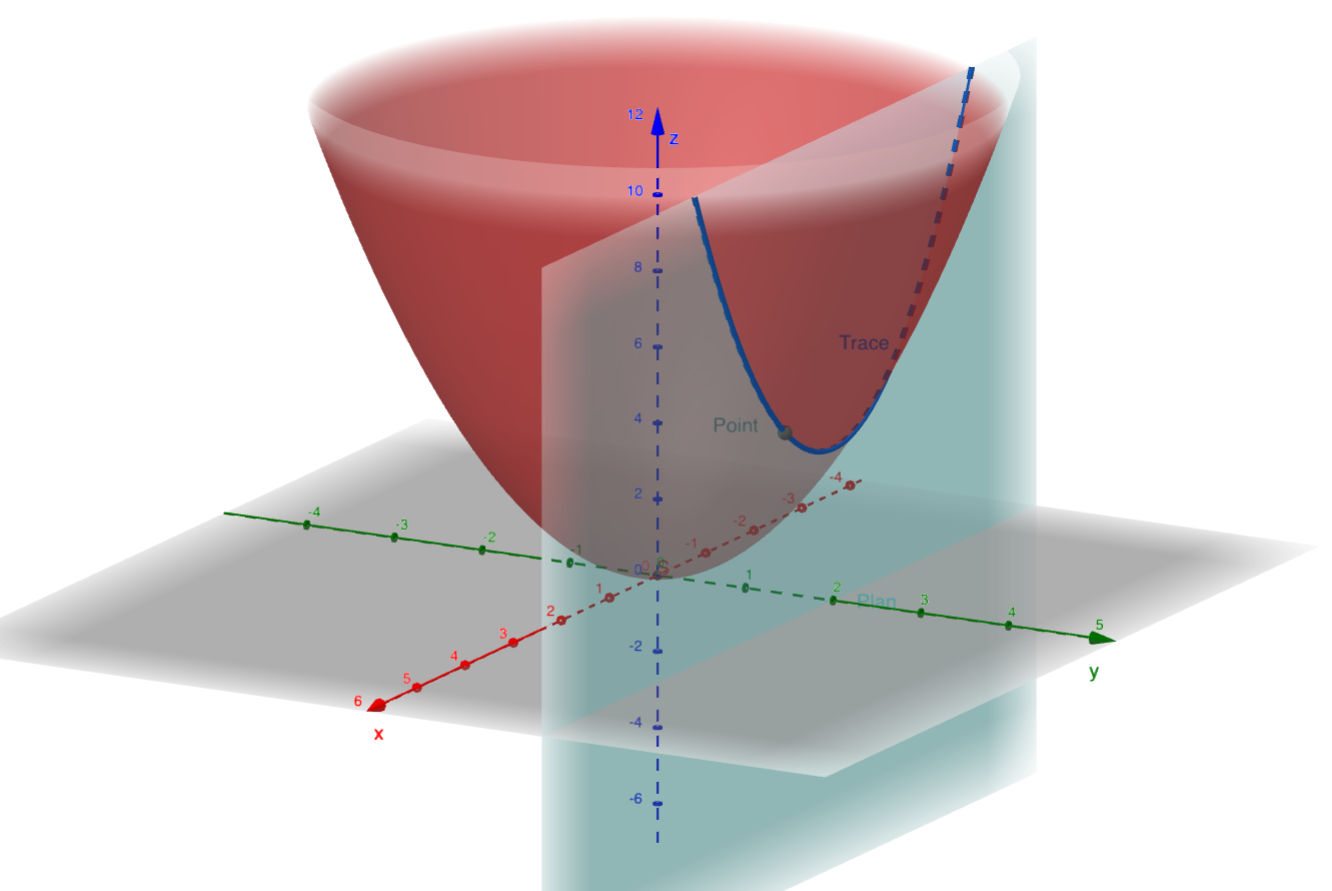
avec le plan d'équation \(y=2\) en bleu pâle, et la trace de la surface dans ce plan en bleu plus foncé.

  1. Cette trace est la parabole d'équation

    \begin{equation*} z=x^2+4 \end{equation*}

    dans le plan d'équation \(y=2\text{.}\)

    En voici une représentation graphique

    avec la tangente au point considéré en mauve.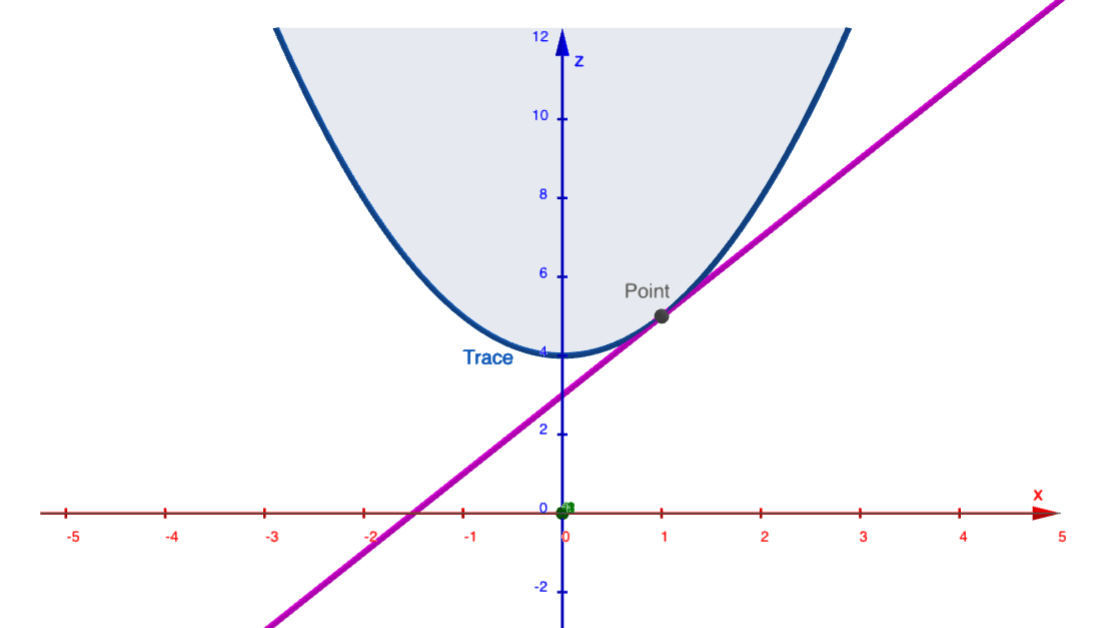

    La pente de la tangente cherchée s'obtient donc en évaluant la dérivée de \(z=x^2+4\) par rapport à \(x\) en \(x=1\text{.}\)

  2. Cette trace est la parabole d'équation

    \begin{equation*} z=1+y^2 \end{equation*}

    dans le plan d'équation \(x=1\text{.}\)

    La pente de la tangente cherchée s'obtient donc en évaluant la dérivée de \(z=1+y^2\) par rapport à \(y\) en \(y=2\text{.}\)

Réponse

  1. Cette pente vaut \(2\text{.}\)

  2. Cette pente vaut \(4\text{.}\)

Solution 1

  1. Suivons l'indication et dérivons l'équation de la trace

    \begin{equation*} z=x^2+4 \end{equation*}

    par rapport à \(x\) :

    \begin{align*} \frac{\mathrm{d}z}{\mathrm{d}x}&=\frac{\mathrm{d}}{\mathrm{d}x}\left(x^2+4\right)\\ &=2x+0\\ &=2x. \end{align*}

    Au point \((1,2,5)\text{,}\) la tangente a donc pour pente

    \begin{equation*} \left.\frac{\mathrm{d}z}{\mathrm{d}x}\right|_{x=1}=2\cdot 1=2. \end{equation*}

  2. De même, suivons l'indication et dérivons l'équation de la trace

    \begin{equation*} z=1+y^2 \end{equation*}

    par rapport à \(y\) :

    \begin{align*} \frac{\mathrm{d}z}{\mathrm{d}y}&=\frac{\mathrm{d}}{\mathrm{d}y}\left(1+y^2\right)\\ &=0+2y\\ &=2y. \end{align*}

    Au point \((1,2,5)\text{,}\) la tangente a donc pour pente

    \begin{equation*} \left.\frac{\mathrm{d}z}{\mathrm{d}y}\right|_{y=2}=2\cdot 2=4. \end{equation*}
Solution 2

  1. On a

    \begin{align*} \frac{\partial z}{\partial x}&=\frac{\partial}{\partial x}\left(x^2+y^2\right)\\ &=2x+0\\ &=2x. \end{align*}

    La pente cherchée vaut donc

    \begin{equation*} \left.\frac{\partial z}{\partial x}\right|_{(x,y)=(1,2)}=2\cdot 1=2. \end{equation*}

  2. On a

    \begin{align*} \frac{\partial z}{\partial y}&=\frac{\partial}{\partial y}\left(x^2+y^2\right)\\ &=0+2y\\ &=2y. \end{align*}

    La pente cherchée vaut donc

    \begin{equation*} \left.\frac{\partial z}{\partial y}\right|_{(x,y)=(1,2)}=2\cdot 2=4. \end{equation*}
Solution 3

La surface S est le graphe de la fonction de deux variables

\begin{equation*} f(x,y)=x^2+y^2 \end{equation*}

dont les dérivées partielles sont

\begin{equation*} f_x(x,y)=\frac{\partial f}{\partial x}=2x \end{equation*}

et

\begin{equation*} f_y(x,y)=\frac{\partial f}{\partial y}=2y. \end{equation*}

  1. La pente cherchée est

    \begin{equation*} f_x(1,2)=2\cdot 1=2. \end{equation*}

  2. La pente cherchée est

    \begin{equation*} f_y(1,2)=2\cdot 2=4. \end{equation*}

On s'intéresse à la fonction de deux variables

\begin{equation*} f(x,y)=\cos(x)\sin(y). \end{equation*}

Représentez le graphe de cette fonction à l'aide de votre logiciel favori.

Sans faire de calculs, déterminez visuellement le signe des dérivées partielles indiquées.

  1. \(f_y(0,1)\text{.}\)

  2. \(f_y(0,2)\text{.}\)

  3. \(f_x(1,2)\text{.}\)

  4. \(f_x(0,2)\text{.}\)

Indication

Commencer par représenter le graphe de cette fonction à l'aide de votre logiciel favori.

Pour chaque dérivée partielle, visualisez la tangente adéquate : sa pente est-elle positive, négative, ou nulle? Faites attention à orienter l'axe de la variable indépendante (\(x\) pour \(f_x\) et \(y\) s'il s'agit de \(f_y\)) vers la droite, et celui de la variable dépendante (\(z\)) vers le haut.

Alternativement, imaginez que vous marchez sur la surface et que la variable \(z\) correspond à votre altitude. Par exemple, pour déterminer le signe de \(f_x(1,2)\text{,}\) rendez-vous au point \((1,2,f(1,2))\text{.}\) Avancez ensuite tout droit dans le sens des \(x\) croissants. Êtes-vous en train de monter ou de descendre?

Réponse

  1. \(f_y(0,1)>0\text{.}\)

  2. \(f_y(0,2)<0\text{.}\)

  3. \(f_x(1,2)<0\text{.}\)

  4. \(f_x(0,2)=0\text{.}\)

Solution

Voici le graphe de la fonction \(f\)

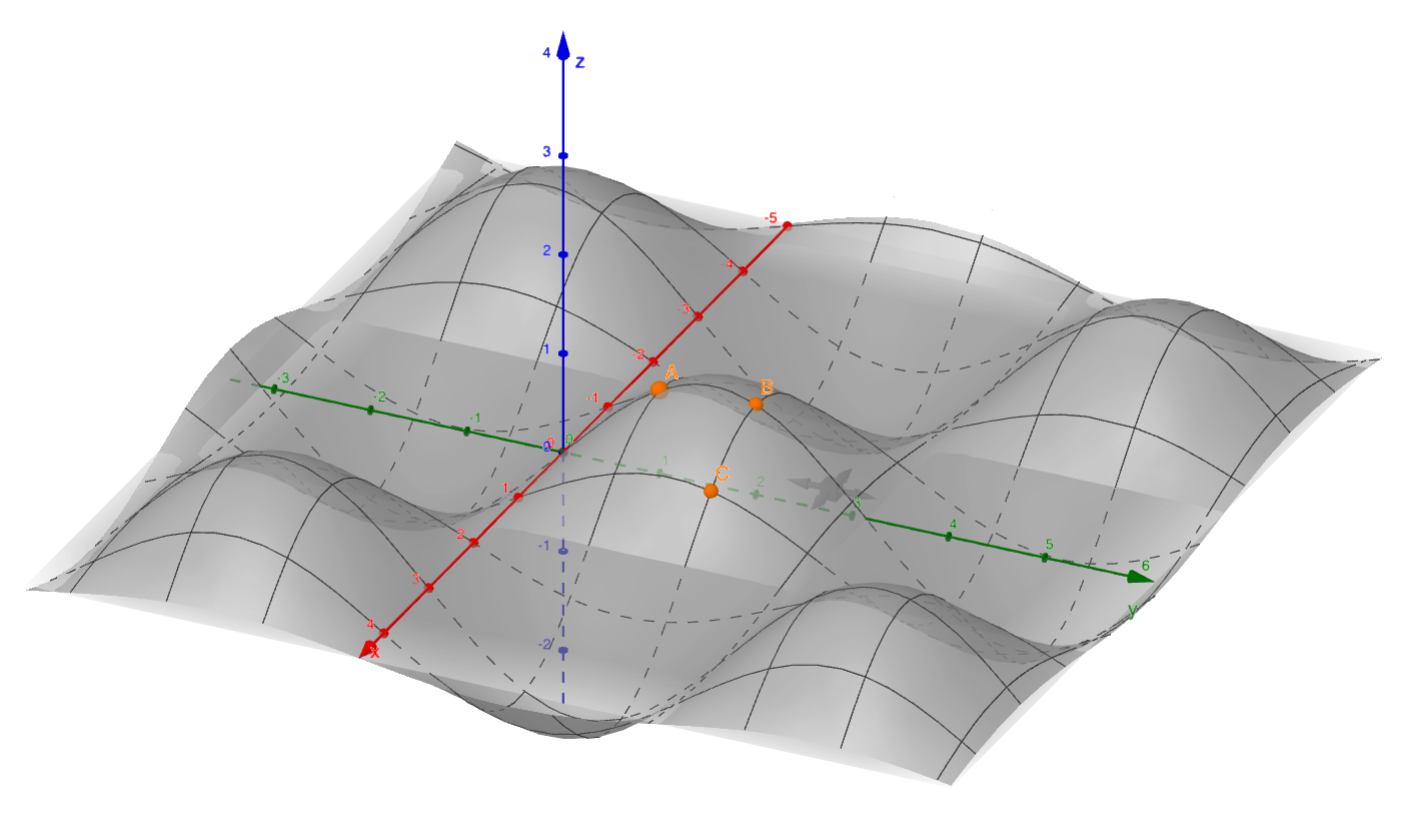
où \(A,B,C\) sont les trois points à considérer.

  • Voici la trace du graphe de la fonction \(f\) dans le plan d'équation

    \begin{equation*} x=0 \end{equation*}

    où les points identifiés sont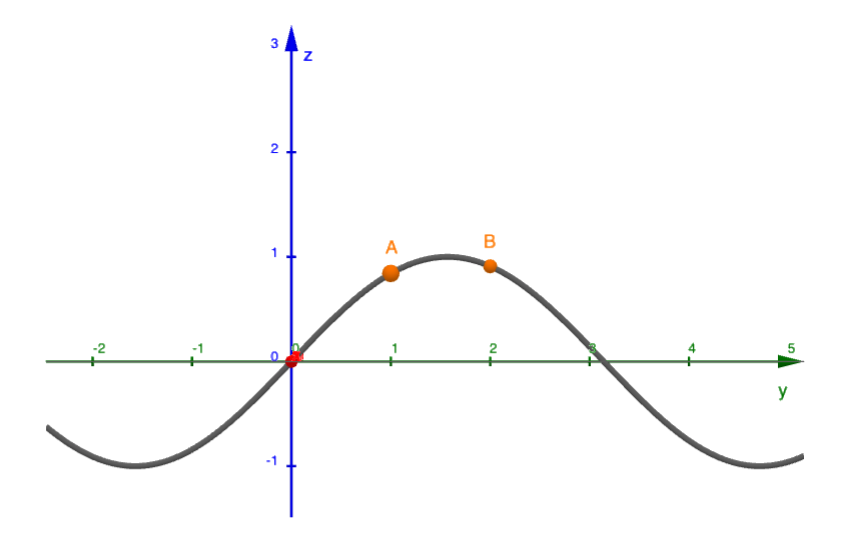

    \begin{equation*} A=(0,1,f(0,1))\quad\text{et}\quad B=(0,2,f(0,2)). \end{equation*}

    1. Comme la tangente au point \(A\) a une pente positive, on a

    \begin{equation*} f_y(0,1)>0. \end{equation*}

    2. Comme la tangente au point \(B\) a une pente négative, on a

    \begin{equation*} f_y(0,2)<0. \end{equation*}

  • Voici la trace du graphe de la fonction \(f\) dans le plan d'équation

    \begin{equation*} y=2 \end{equation*}

    où les points identifiés sont

    \begin{equation*} C=(1,2,f(1,2))\quad\text{et}\quad B=(0,2,f(0,2)). \end{equation*}

    3. Comme la tangente au point \(C\) a une pente négative, on a

    \begin{equation*} f_x(1,2)<0. \end{equation*}

    4. Comme la tangente au point \(B\) est horizontale, on a

    \begin{equation*} f_x(0,2)=0. \end{equation*}

  1. Soit \(f\) une fonction d'une seule variable \(x\text{.}\)

    Définissez le nombre

    \begin{equation*} f'(2) \end{equation*}

    à l'aide d'une limite. Comment l'appelle-t-on? Comment se note-t-il si on utilise des \(\mathrm{d}\;\text{?}\)

  2. Soit \(f\) une fonction de deux variables \(x,y\text{.}\)

    Définissez le nombre

    \begin{equation*} f_x(2,1) \end{equation*}

    à l'aide d'une limite. Comment l'appelle-t-on? Comment se note-t-il si on utilise des \(\partial\;\text{?}\)

Indication

  1. Consultez votre cours de calcul différentiel préféré.

  2. Ajoutez une deuxième variable et donnez-lui la valeur

    \begin{equation*} y=1 \end{equation*}

    partout, ce qui revient à travailler dans le plan d'équation \(y=1\) et à se ramener à une seule variable \(x\text{.}\)

Solution

  1. Le nombre \(f'(2)\) est égal à la limite suivante, si elle existe :

    \begin{equation*} f'(2)=\lim_{x\rightarrow 2}\frac{f(x)-f(2)}{x-2}. \end{equation*}

    On l'appelle dérivée de \(f\) en \(x=2\) et on le note aussi

    \begin{equation*} f'(2)=\left.\frac{\mathrm{d}f}{\mathrm{d}x}\right|_{x=2}. \end{equation*}

  2. Le nombre \(f_x(2,1)\) est égal à la limite suivante, si elle existe :

    \begin{equation*} f_x(2,1)=\lim_{x\rightarrow 2}\frac{f(x,1)-f(2,1)}{x-2}. \end{equation*}

    On l'appelle dérivée partielle de \(f\) par rapport à \(x\) au point \((x,y)=(2,1)\) et on le note aussi

    \begin{equation*} f_x(2,1)=\left.\frac{\partial f}{\partial x}\right|_{(x,y)=(2,1)}. \end{equation*}

Utilisez le diagramme de courbes de niveau

de la fonction de deux variables \(f\) pour estimer les nombres

\begin{equation*} f_x(2,1)\quad\text{et}\quad f_y(2,1). \end{equation*}
Indication

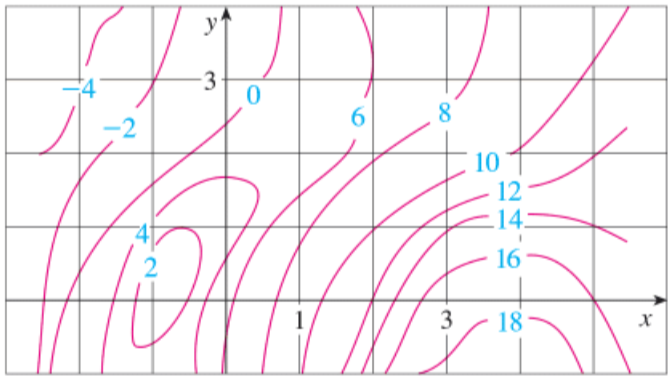
Quand on ne connaît qu'un nombre fini de valeurs prises par la fonction \(f\text{,}\) la dérivée partielle

\begin{equation*} f_x(2,1)=\frac{\partial f}{\partial x}(2,1)=\lim_{x\rightarrow 2}\frac{f(x,1)-f(2,1)}{x-2} \end{equation*}

peut être estimée à l'aide de quotients du type

\begin{equation*} \frac{\Delta z}{\Delta x}=\frac{f(x,1)-f(2,1)}{x-2} \end{equation*}

où la valeur de \(x\) est assez proche de \(2\) et permet de lire la valeur de \(f(x,1)\text{.}\)

Dans le cas de ce diagramme de courbes de niveau, voici un exemple de stratégie pour effectuer une estimation de

\begin{equation*} f_x(2,1). \end{equation*}

  1. Repérez le point \((2,1)\) et notez la valeur de \(f(2,1)\text{.}\)

  2. Déplacez-vous horizontalement vers la gauche jusqu'à la première courbe de niveau rencontrée et notez la valeur de \(f\) correspondante : vous avez votre \(\Delta z\text{.}\)

  3. Mesurez le déplacement horizontal algébrique : vous avez votre \(\Delta x\text{.}\)

  4. Faites la division. Vous avez votre première estimation :

    \begin{equation*} f_x(2,1)\approx\frac{\Delta z}{\Delta x}. \end{equation*}

  5. Répétez les étapes précédentes en vous déplaçant cette fois-ci horizontalement vers la droite : vous obtenez une deuxième estimation.

  6. Faites la moyenne de vos deux estimations.

Réponse

Avec ma démarche, et mes mesures, j'ai trouvé

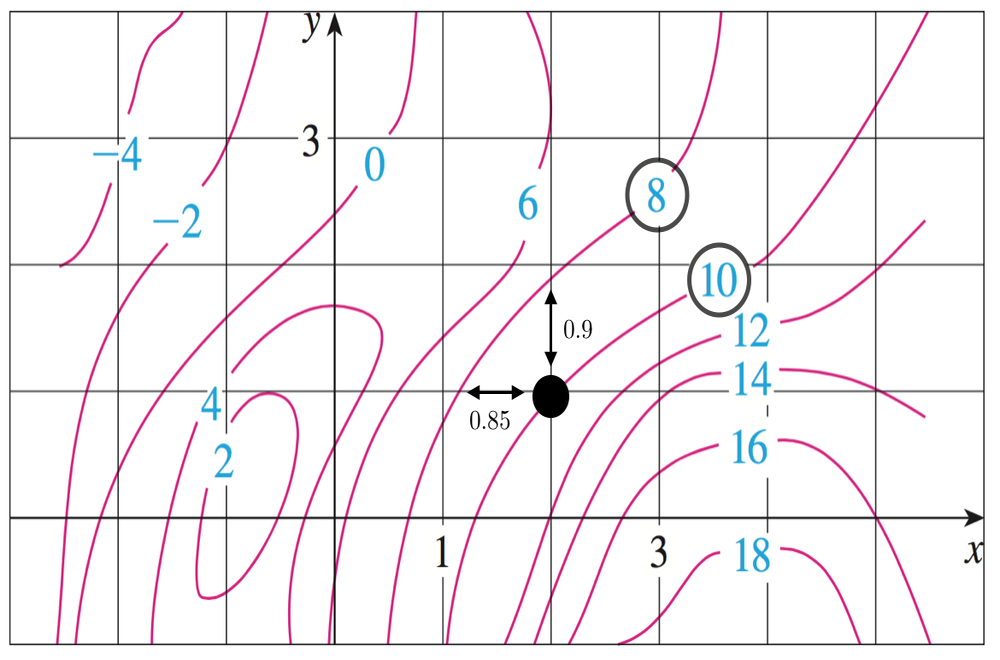
\begin{equation*} f_x(2,1)\approx 2{,}65\quad\text{et}\quad f_y(2,1)\approx -2{,}11. \end{equation*}
Solution

Voici une illustration de ce que nous allons faire :

  • Pour estimer \(f_x(2,1)\text{,}\) commençons par nous déplacer horizontalement vers la gauche en partant du point \((2,1)\) où \(z=1\text{,}\) jusqu'à la première courbe de niveau rencontrée où \(z=8\text{.}\) On obtient

    \begin{equation*} \frac{\Delta z}{\Delta x}=\frac{8-10}{-0{,}85}\approx 2{,}35. \end{equation*}

    En faisant la même chose, mais en se déplaçant vers la droite, on trouve

    \begin{equation*} \frac{\Delta z}{\Delta x}=\frac{12-10}{0{,}68}\approx 2{,}94. \end{equation*}

    Pour finir, on prend la moyenne de ces deux valeurs :

    \begin{equation*} f_x(2,1)\approx\frac{2{,}35+2{,}94}{2}\approx 2{,}65. \end{equation*}

  • Pour estimer \(f_y(2,1)\text{,}\) commençons par nous déplacer verticalement vers le haut en partant du point \((2,1)\) où \(z=1\text{,}\) jusqu'à la première courbe de niveau rencontrée où \(z=8\text{.}\) On obtient

    \begin{equation*} \frac{\Delta z}{\Delta y}=\frac{8-10}{0{,}9}\approx -2{,}22. \end{equation*}

    En faisant la même chose, mais en se déplaçant vers la bas, on trouve

    \begin{equation*} \frac{\Delta z}{\Delta y}=\frac{12-10}{-1}=-2. \end{equation*}

    Pour finir, on prend la moyenne de ces deux valeurs :

    \begin{equation*} f_y(2,1)\approx\frac{-2{,}22+(-2)}{2}\approx -2{,}11. \end{equation*}

Calculez toutes les dérivées partielles de

  1. \(f\) si

    \begin{equation*} f(x,y)=3x+2y^2-4xy. \end{equation*}

  2. \(z\) si

    \begin{equation*} z=x\cos(x+y^2). \end{equation*}

  3. \(u\) si

    \begin{equation*} u(x,y,z)=x^2-5xe^y+z\sin(x). \end{equation*}

  4. \(f\) si

    \begin{equation*} f(x,y)=x^y. \end{equation*}

  5. \(w\) si

    \begin{equation*} w=\frac{e^v}{u+v^2}. \end{equation*}
Indication

Une fonction \(f\) qui dépend de deux variables \(x\) et \(y\) admet deux dérivées partielles notées

\begin{equation*} \frac{\partial f}{\partial x}=f_x\quad\text{et}\quad\frac{\partial f}{\partial y}=f_y. \end{equation*}

  • Pour calculer \(f_x\text{,}\) on traite \(y\) comme une constante et on dérive par rapport à \(x\text{.}\)

  • Pour calculer \(f_y\text{,}\) on traite \(x\) comme une constante et on dérive par rapport à \(y\text{.}\)

Réponse

  1. On trouve

    \begin{equation*} f_x(x,y)=3-4y\quad\text{et}\quad f_y(x,y)=4y-4x. \end{equation*}

  2. On trouve

    \begin{equation*} \frac{\partial z}{\partial x}=\cos(x+y^2)-x\sin(x+y^2)\quad\text{et}\quad\frac{\partial z}{\partial y}=-2xy\sin(x+y^2). \end{equation*}

  3. On trouve

    \begin{equation*} \frac{\partial u}{\partial x}=2x-5e^y+z\cos x,\quad\frac{\partial u}{\partial y}=-5xe^y\quad\text{et}\quad\frac{\partial u}{\partial z}=\sin x. \end{equation*}

  4. On trouve

    \begin{equation*} f_x(x,y)=yx^{y-1}\quad\text{et}\quad f_y(x;y)=x^y\ln x. \end{equation*}

  5. On trouve

    \begin{equation*} \frac{\partial w}{\partial u}=-\frac{e^v}{(u+v^2)^2}\quad\text{et}\quad\frac{\partial w}{\partial v}=\frac{e^v(u+v^2-2v)}{(u+v^2)^2}. \end{equation*}
Solution

  1. On a

    \begin{align*} f_x(x,y)&=\frac{\partial}{\partial x}\left(3x+2y^2-4xy\right)\\ &=\frac{\partial}{\partial x}\left(3x\right)+\frac{\partial}{\partial x}\left(2y^2\right)-\frac{\partial}{\partial x}\left(4xy\right)\\ &=3+0-4y\\ &=3-4y \end{align*}

    et

    \begin{align*} f_y(x,y)&=\frac{\partial}{\partial y}\left(3x+2y^2-4xy\right)\\ &=\frac{\partial}{\partial y}\left(3x\right)+\frac{\partial}{\partial y}\left(2y^2\right)-\frac{\partial}{\partial y}\left(4xy\right)\\ &=0+4y-4x\\ &=4y-4x. \end{align*}

  2. On a

    \begin{align*} \frac{\partial z}{\partial x}&=\frac{\partial}{\partial x}\left(x\cdot\cos(x+y^2)\right)\\ &=\frac{\partial}{\partial x}\left(x\right)\cdot\cos(x+y^2)+x\cdot\frac{\partial}{\partial x}\left(\cos(x+y^2)\right)\\ &=1\cdot\cos(x+y^2)+x\cdot\left(-\sin(x+y^2)\right)\frac{\partial}{\partial x}\left(x+y^2\right)\\ &=1\cdot\cos(x+y^2)+x\cdot\left(-\sin(x+y^2)\right)\cdot(1+0)\\ &=\cos(x+y^2)-x\sin(x+y^2) \end{align*}

    et

    \begin{align*} \frac{\partial z}{\partial y}&=\frac{\partial}{\partial y}\left(x\cdot\cos(x+y^2)\right)\\ &=x\cdot\frac{\partial}{\partial y}\left(\cos(x+y^2)\right)\\ &=x\cdot\left(-\sin(x+y^2)\right)\frac{\partial}{\partial y}\left(x+y^2\right)\\ &=x\cdot\left(-\sin(x+y^2)\right)\cdot(0+2y)\\ &=-2xy\sin(x+y^2). \end{align*}

  3. On a

    \begin{align*} \frac{\partial u}{\partial x}&=\frac{\partial}{\partial x}\left(x^2-5xe^y+z\sin x\right)\\ &=\frac{\partial}{\partial x}\left(x^2\right)-\frac{\partial}{\partial x}\left(5xe^y\right)+\frac{\partial}{\partial x}\left(z\sin x\right)\\ &=2x-5e^y+z\cos x, \end{align*}

    puis

    \begin{align*} \frac{\partial u}{\partial y}&=\frac{\partial}{\partial y}\left(x^2-5xe^y+z\sin x\right)\\ &=\frac{\partial}{\partial y}\left(x^2\right)-\frac{\partial}{\partial y}\left(5xe^y\right)+\frac{\partial}{\partial y}\left(z\sin x\right)\\ &=0-5xe^y+0\\ &=-5xe^y, \end{align*}

    et enfin

    \begin{align*} \frac{\partial u}{\partial z}&=\frac{\partial}{\partial z}\left(x^2-5xe^y+z\sin x\right)\\ &=\frac{\partial}{\partial z}\left(x^2\right)-\frac{\partial}{\partial z}\left(5xe^y\right)+\frac{\partial}{\partial z}\left(z\sin x\right)\\ &=0-0+\sin x\\ &=\sin x. \end{align*}

  4. On a

    \begin{align*} f_x(x,y)&=\frac{\partial}{\partial x}\left(x^y\right)\\ &=yx^{y-1} \end{align*}

    et

    \begin{align*} f_y(x,y)&=\frac{\partial}{\partial y}\left(x^y\right)\\ &=x^y\ln y. \end{align*}

  5. On a

    \begin{align*} \frac{\partial w}{\partial u}&=\frac{\partial}{\partial u}\left(\frac{e^v}{u+v^2}\right)\\ &=\frac{\frac{\partial}{\partial u}\left(e^v\right)\cdot(u+v^2)-e^v\cdot\frac{\partial}{\partial u}\left(u+v^2\right)}{(u+v^2)^2}\\ &=\frac{0\cdot(u+v^2)-e^v\cdot 1}{(u+v^2)^2}\\ &=-\frac{e^v}{(u+v^2)^2} \end{align*}

    et

    \begin{align*} \frac{\partial w}{\partial v}&=\frac{\partial}{\partial v}\left(\frac{e^v}{u+v^2}\right)\\ &=\frac{\frac{\partial}{\partial v}\left(e^v\right)\cdot(u+v^2)-e^v\cdot\frac{\partial}{\partial v}\left(u+v^2\right)}{(u+v^2)^2}\\ &=\frac{e^v\cdot(u+v^2)-e^v\cdot(2v)}{(u+v^2)^2}\\ &=\frac{e^v(u+v^2-2v)}{(u+v^2)^2}. \end{align*}

Trouvez toutes les dérivées partielles secondes de la fonction de deux variables

\begin{equation*} f(x,y)=x^2y+3y^2. \end{equation*}

La conclusion du théorème de Clairaut est-elle vérifiée?

Indication

  • Commencez par calculer la dérivée première

    \begin{equation*} \frac{\partial f}{\partial x}=f_x. \end{equation*}

    Dérivez ensuite cette fonction par rapport à \(x\) pour obtenir

    \begin{equation*} \frac{\partial^2 f}{\partial x^2}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial}{\partial x}\left(f_x\right)=(f_x)_x=f_{xx}, \end{equation*}

    puis par rapport à \(y\) pour obtenir

    \begin{equation*} \frac{\partial^2 f}{\partial y\partial x}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial}{\partial y}\left(f_x\right)=(f_x)_y=f_{xy}. \end{equation*}

  • Après cela, calculez la dérivée première

    \begin{equation*} \frac{\partial f}{\partial y}=f_y. \end{equation*}

    Dérivez ensuite cette fonction par rapport à \(y\) pour obtenir

    \begin{equation*} \frac{\partial^2 f}{\partial y^2}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial}{\partial y}\left(f_y\right)=(f_y)_y=f_{yy}, \end{equation*}

    puis par rapport à \(x\) pour obtenir

    \begin{equation*} \frac{\partial^2 f}{\partial x\partial y}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial}{\partial x}\left(f_y\right)=(f_y)_x=f_{yx}. \end{equation*}

  • Pour finir, comparez les dérivées mixtes \(f_{xy}=\dfrac{\partial^2 f}{\partial y\partial x}\) et \(f_{yx}=\dfrac{\partial^2 f}{\partial x\partial y}\text{.}\)

Réponse

On obtient

\begin{equation*} \begin{matrix} f_{xx}=\dfrac{\partial^2f}{\partial x^2}=2y&\quad f_{yx}=\dfrac{\partial^2f}{\partial x\partial y}=2x\\ f_{xy}=\dfrac{\partial^2f}{\partial y\partial x}=2x&\quad f_{yy}=\dfrac{\partial^2f}{\partial y^2}=6 \end{matrix} \end{equation*}

et la conclusion du théorème de Clairaut est vérifiée, car on a bien

\begin{equation*} f_{xy}=f_{yx}. \end{equation*}
Solution

  • D'une part, on a

    \begin{equation*} f_x=\frac{\partial}{\partial x}(x^2y+3y^2)=2xy, \end{equation*}

    d'où

    \begin{align*} f_{xx}&=\frac{\partial}{\partial x}\left(f_x\right)\\ &=\frac{\partial}{\partial x}\left(2xy\right)\\ &=2y \end{align*}

    et

    \begin{align*} f_{xy}&=\frac{\partial}{\partial y}\left(f_x\right)\\ &=\frac{\partial}{\partial y}\left(2xy\right)\\ &=2x. \end{align*}

  • D'autre part, on a

    \begin{equation*} f_y=\frac{\partial}{\partial y}(x^2y+3y^2)=x^2+6y, \end{equation*}

    d'où

    \begin{align*} f_{yy}&=\frac{\partial}{\partial y}\left(f_y\right)\\ &=\frac{\partial}{\partial y}\left(x^2+6y\right)\\ &=6 \end{align*}

    et

    \begin{align*} f_{yx}&=\frac{\partial}{\partial x}\left(f_y\right)\\ &=\frac{\partial}{\partial x}\left(x^2+6y\right)\\ &=2x. \end{align*}

En résumé, on obtient

\begin{equation*} \begin{matrix} f_{xx}=\dfrac{\partial^2f}{\partial x^2}=2y&\quad f_{yx}=\dfrac{\partial^2f}{\partial x\partial y}=2x\\ f_{xy}=\dfrac{\partial^2f}{\partial y\partial x}=2x&\quad f_{yy}=\dfrac{\partial^2f}{\partial y^2}=6 \end{matrix} \end{equation*}

et la conclusion du théorème de Clairaut est vérifiée, car on a bien

\begin{equation*} f_{xy}=f_{yx}. \end{equation*}

Pour la fonction

\begin{equation*} f(x,y)=x^2y+3y^2 \end{equation*}

de l'exercice précédent 4.1.6, calculez

\begin{equation*} \frac{\partial^3f}{\partial y^2\partial x} \end{equation*}

de deux façons différentes au moins.

Indication

En partant des calculs faits à l'exercice précédent 4.1.6, calculez d'abord

\begin{equation*} \frac{\partial^3f}{\partial y^2\partial x} \end{equation*}

en suivant la définition, c'est-à-dire

\begin{equation*} \frac{\partial^3f}{\partial y^2\partial x}=\frac{\partial}{\partial y}\left(\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)\right)=f_{xyy}. \end{equation*}

Puis utilisez le théorème de Clairaut pour justifier la permutation de l'ordre des dérivations et aboutir au même résultat en empruntant un chemin différent.

Réponse

Quel que soit l'ordre des dérivations choisi, on trouve

\begin{equation*} \frac{\partial^3f}{\partial y^2\partial x}=f_{xyy}=f_{yxy}=f_{yyx}=0. \end{equation*}
Solution

Rappelons d'abord les calculs

\begin{equation*} \begin{matrix} f_{xx}=\dfrac{\partial^2f}{\partial x^2}=2y&\quad f_{yx}=\dfrac{\partial^2f}{\partial x\partial y}=2x\\ f_{xy}=\dfrac{\partial^2f}{\partial y\partial x}=2x&\quad f_{yy}=\dfrac{\partial^2f}{\partial y^2}=6 \end{matrix} \end{equation*}

effectués à l'exercice précédent 4.1.6.

  • Par définition, on a

    \begin{align*} \frac{\partial^3f}{\partial y^2\partial x}&=\frac{\partial}{\partial y}\left(\frac{\partial^2f}{\partial y\partial x}\right)\\ &=\frac{\partial}{\partial y}\left(2x\right)\\ &=0. \end{align*}

  • Grâce au théorème de Clairaut, on peut permuter les dérivations partielles et prendre ainsi un chemin différent :

    \begin{align*} \frac{\partial^3f}{\partial y^2\partial x}&=f_{xyy}\\ &=f_{yyx}\\ &=\frac{\partial}{\partial x}\left(f_{yy}\right)\\ &=\frac{\partial}{\partial x}\left(6\right)\\ &=0. \end{align*}
Synthèse 4.1.2.

On considère la fonction de deux variables

\begin{equation*} f(x,y)=\arctan\left(\frac{y}{x}\right). \end{equation*}
(a)

Dériver \(f(x,y)\) par rapport à \(y\text{.}\)

Solution

Commençons par remarquer que

\begin{equation*} \frac{\partial}{\partial y}\left(\frac{y}{x}\right)=\frac{1}{x}. \end{equation*}

Par dérivation en chaîne, on obtient alors

\begin{align*} f_y(x,y)&=\frac{\partial}{\partial y}\left(\arctan\left(\frac{y}{x}\right)\right)\\ &=\frac{1}{1+\left(\frac{y}{x}\right)^2}\cdot\frac{\partial}{\partial y}\left(\frac{y}{x}\right)\\ &=\frac{1}{1+\frac{y^2}{x^2}}\cdot\frac{1}{x}\\ &=\frac{x}{x^2+y^2}. \end{align*}
(b)

Dériver \(f(x,y)\) par rapport à \(x\text{.}\)

Solution

Commençons par remarquer que

\begin{align*} \frac{\partial}{\partial x}\left(\frac{y}{x}\right)&=\frac{\partial}{\partial x}\left(yx^{-1}\right)\\ &=y\cdot\frac{\partial}{\partial x}\left(x^{-1}\right)\\ &=y\cdot(-1)\cdot x^{-2}\\ &=-\frac{y}{x^2}. \end{align*}

Par dérivation en chaîne, on obtient alors

\begin{align*} f_x(x,y)&=\frac{\partial}{\partial x}\left(\arctan\left(\frac{y}{x}\right)\right)\\ &=\frac{1}{1+\left(\frac{y}{x}\right)^2}\cdot\frac{\partial}{\partial x}\left(\frac{y}{x}\right)\\ &=\frac{1}{1+\frac{y^2}{x^2}}\cdot\left(-\frac{y}{x^2}\right)\\ &=-\frac{y}{x^2+y^2}. \end{align*}
(c)

Représenter l'intersection du graphe de la fonction \(f\) avec le plan d'équation \(y=3\text{.}\) Comment appelle-t-on cette courbe?

Solution

Voici le graphe de la fonction

avec le plan en bleu ciel et leur intersection en noir. On appelle cette intersection la trace du graphe dans le plan d'équation \(y=3\text{.}\)

(d)

Interpréter graphiquement le nombre \(f_x(2,3)\text{.}\) Dire sans calcul s'il est positif, négatif ou nul.

Solution

Le nombre \(f_x(2,3)\) est la pente de la tangente à la trace du graphe de la fonction \(f\) avec le plan d'équation \(y=3\) au point \((2,3,f(2,3))\text{.}\)

Voici la représentation graphique de la trace en question

dans le plan d'équation \(y=3\text{.}\)

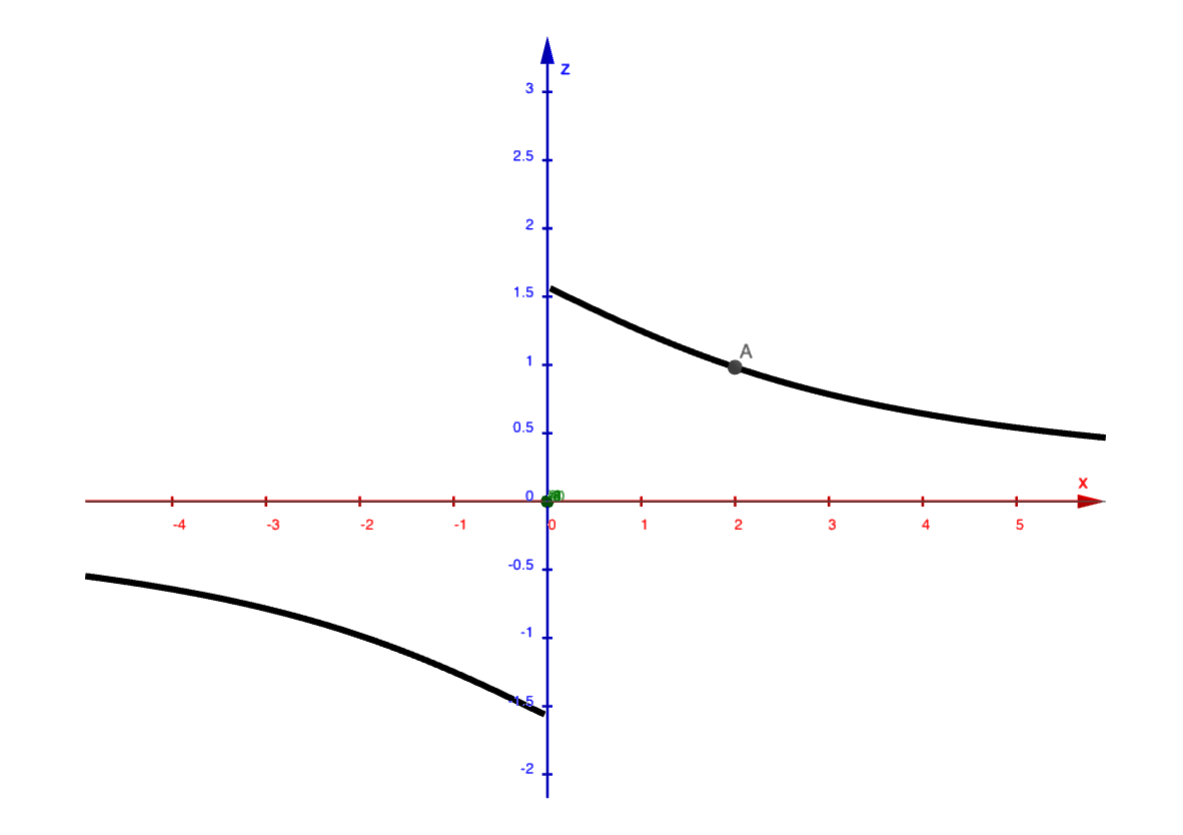
La pente de la tangente au point donné est clairement négative. On en déduit donc que

\begin{equation*} f_x(2,3)<0 \end{equation*}

sans calculs.

(e)

Définir \(f_x(2,3)\) à l'aide d'une limite.

Solution

Si la limite suivante existe, alors

\begin{equation*} f_x(2,3)=\lim_{x\rightarrow 2}\frac{f(x,3)-f(2,3)}{x-2}. \end{equation*}
(f)

Sachant que

\begin{equation*} f(2;3)\approx 0{,}983\quad\text{et}\quad f(2{,}1;3)\approx 0{,}960 \end{equation*}

donner une estimation de \(f_x(2,3)\) sans dériver.

Solution

Comme

\begin{equation*} f_x(2,3)=\lim_{x\rightarrow 2}\frac{f(x,3)-f(2,3)}{x-2} \end{equation*}

on peut estimer cette limite par

\begin{align*} \frac{f(2{,}1;3)-f(2;3)}{2{,}1-2}&\quad\approx\quad\frac{0{,}960-0{,}983}{0{,}1}\\ &\quad=\quad-0{,}023\cdot 10\\ &\quad=\quad-0{,}23. \end{align*}
(g)

Donner la valeur exacte de \(f_x(2,3)\) et comparer avec l'estimation obtenue à la question précédente.

Solution

On a déjà calculé la dérivée partielle

\begin{equation*} f_x(x,y)=-\frac{y}{x^2+y^2} \end{equation*}

plus haut. Il en découle que

\begin{align*} f_x(2,3)&=-\frac{3}{2^2+3^2}\\ &=-\frac{3}{13}\\ &=-0{,}230\,769\ldots \end{align*}

On avait donc deux déjà deux décimales correctes avec l'estimation précédente.

(h)

Vérifier que la fonction \(f\) satisfait la conclusion du théorème de Clairaut.

Solution

On a déjà calculé

\begin{equation*} f_x=-\frac{y}{x^2+y^2}\quad\text{et}\quad f_y=\frac{x}{x^2+y^2}. \end{equation*}

Alors

\begin{align*} f_{xy}&=(f_x)_y\\ &=\frac{\partial}{\partial y}(f_x)\\ &=\frac{\partial}{\partial y}\left(-\frac{y}{x^2+y^2}\right)\\ &=-\frac{\partial}{\partial y}\left(\frac{y}{x^2+y^2}\right)\\ &=-\frac{\frac{\partial}{\partial y}(y)\cdot(x^2+y^2)-y\cdot\frac{\partial}{\partial y}(x^2+y^2)}{(x^2+y^2)^2}\\ &=-\frac{1\cdot(x^2+y^2)-y\cdot 2y}{(x^2+y^2)^2}\\ &=-\frac{x^2+y^2-2y^2}{(x^2+y^2)^2}\\ &=\frac{y^2-x^2}{(x^2+y^2)^2} \end{align*}

et

\begin{align*} f_{yx}&=(f_y)_x\\ &=\frac{\partial}{\partial x}(f_y)\\ &=\frac{\partial}{\partial y}\left(\frac{x}{x^2+y^2}\right)\\ &=\frac{\frac{\partial}{\partial x}(x)\cdot(x^2+y^2)-x\cdot\frac{\partial}{\partial x}(x^2+y^2)}{(x^2+y^2)^2}\\ &=\frac{1\cdot(x^2+y^2)-x\cdot 2x}{(x^2+y^2)^2}\\ &=\frac{x^2+y^2-2x^2}{(x^2+y^2)^2}\\ &=\frac{y^2-x^2}{(x^2+y^2)^2}. \end{align*}

Donc on a

\begin{equation*} f_{xy}=f_{yx} \end{equation*}

et la conclusion du théorème de Clairaut est bien vérifiée.

Si vous souhaitez en faire plus ou disposer de plus d'exemples, vous pouvez consulter les exercices 6, 10 (déjà fait plus haut), 18, 20, 22, 28, 32, 34, 42, 46, 48, 50, 58, 76, 78ab, 80abc dont voici les solutions.

Sinon, passez directement aux exercices prioritaires de cette section.

Remarque : Voici le document distribué les sessions précédentes. Et en voilà le solutionnaire.