Calcul avancé

Voici en rouge le cercle d'équation

et en bleu les lignes de niveau de \(f(x,y)=x-y\)

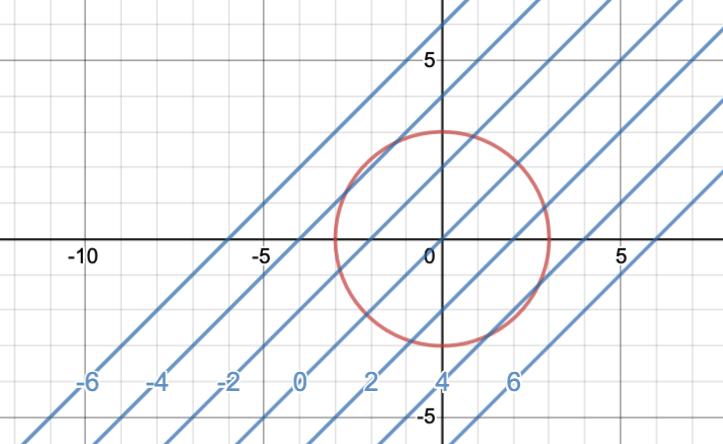
On voit ainsi que le maximum de \(f\) sous la contrainte \(x^2+y^2=9\) est atteint dans le quatrième quadrant, au point du cercle qui vérifie \(y=-x\text{.}\)

On doit donc résoudre le système de deux équations

qui donne

Le point où le maximum est obtenu est donc

et le maximum cherché vaut

1. Commençons par calculer les gradients de

   \begin{equation*} f(x,y)=x-y\quad\text{et}\quad g(x,y)=x^2+y^2. \end{equation*}

   Cela donne

   \begin{equation*} \nabla f=\begin{bmatrix}1\\-1\end{bmatrix}\quad\text{et}\quad\nabla g=\begin{bmatrix}2x\\2y\end{bmatrix}. \end{equation*}

   On doit donc résoudre le système

   \begin{equation*} \begin{cases}\nabla f=\lambda\nabla g\\g(x,y)=9\end{cases} \end{equation*}

   qui donne les trois équations suivantes

   \begin{alignat*}{2} (E_1)\quad&& 1 & {}={} 2\lambda x\\ (E_2)\quad&& -1 & {}={} 2\lambda y\\ (E_3)\quad&&x^2+y^2 & {}={} 9 \end{alignat*}

   d'où

   \begin{equation*} x=-y=\frac{1}{2\lambda} \end{equation*}

   par \((E_1)\) et \((E_2)\text{.}\)

   Par \((E_3)\text{,}\) il en découle que

   \begin{align*} x^2+(-x)^2=9&\quad\Leftrightarrow\quad 2x^2=9\\ &\quad\Leftrightarrow\quad x^2=\frac{9}{2}\\ &\quad\Leftrightarrow\quad x=\pm\sqrt{\frac{9}{2}}\\ &\quad\Leftrightarrow\quad x=\pm\frac{3\sqrt{2}}{2}. \end{align*}

   On obtient ainsi les deux points

   \begin{equation*} \left(\frac{3\sqrt{2}}{2},-\frac{3\sqrt{2}}{2}\right)\quad\text{et}\quad\left(-\frac{3\sqrt{2}}{2},\frac{3\sqrt{2}}{2}\right). \end{equation*}

2. On évalue maintenant \(f\) en chacun de ces points :

   \begin{align*} f\left(\frac{3\sqrt{2}}{2},-\frac{3\sqrt{2}}{2}\right)&=\frac{3\sqrt{2}}{2}-\left(-\frac{3\sqrt{2}}{2}\right)\\ &=\frac{3\sqrt{2}}{2}+\frac{3\sqrt{2}}{2}\\ &=3\sqrt{2} \end{align*}

   et

   \begin{align*} f\left(-\frac{3\sqrt{2}}{2},\frac{3\sqrt{2}}{2}\right)&=-\frac{3\sqrt{2}}{2}-\frac{3\sqrt{2}}{2}\\ &=-3\sqrt{2}. \end{align*}

3. Le maximum cherché vaut donc \(3\sqrt{2}\text{,}\) et le minimum \(-3\sqrt{2}\text{.}\)

1. Commençons par calculer les gradients de

   \begin{equation*} f(x,y,z)=x^4+y^4+z^4\quad\text{et}\quad g(x,y,z)=x^2+y^2+z^2. \end{equation*}

   Cela donne

   \begin{equation*} \nabla f=\begin{bmatrix}4x^3\\4y^3\\4z^3\end{bmatrix}\quad\text{et}\quad\nabla g=\begin{bmatrix}2x\\2y\\2z\end{bmatrix}. \end{equation*}

   On doit donc résoudre le système

   \begin{equation*} \begin{cases}\nabla f=\lambda\nabla g\\g(x,y,z)=1\end{cases} \end{equation*}

   qui donne les quatre équations suivantes

   \begin{alignat*}{2} (E_1)\quad && 2x^3 & {}={} \lambda x\\ (E_2)\quad && 2y^3 & {}={} \lambda y\\ (E_3)\quad && 2z^3 & {}={} \lambda z\\ (E_4)\quad &&x^2+y^2+z^2 & {}={} 1. \end{alignat*}

   • Cas 1 : Aucun coordonnée nulle, càd \(xyz\neq 0\text{.}\)

     Alors \((E_1),(E_2),(E_3)\) entraînent

     \begin{equation*} x^2=y^2=z^2=\frac{\lambda}{2} \end{equation*}

     puis \((E_4)\) donne

     \begin{equation*} 3x^2=1\quad\text{d'où}\quad x^2=\frac{1}{3}. \end{equation*}

     Ce cas conduit donc aux huit points suivants

     \begin{equation*} \left(\pm\frac{1}{\sqrt{3}},\pm\frac{1}{\sqrt{3}},\pm\frac{1}{\sqrt{3}}\right). \end{equation*}

   • Cas 2 : Une coordonnée nulle.

     Commençons par le sous-cas où \(x=0\) et \(yz\neq 0\text{.}\)

     Alors \((E_2),(E_3)\) entraînent

     \begin{equation*} y^2=z^2=\frac{\lambda}{2} \end{equation*}

     puis \((E_4)\) donne

     \begin{equation*} 2y^2=1\quad\text{d'où}\quad y^2=\frac{1}{2}. \end{equation*}

     Ce sous-cas conduit donc aux quatre points suivants

     \begin{equation*} \left(0,\pm\frac{1}{\sqrt{2}},\pm\frac{1}{\sqrt{2}}\right). \end{equation*}

     Et pour des raisons de symétrie, on ajoute aussi à ce cas les points

     \begin{equation*} \left(\pm\frac{1}{\sqrt{2}},0,\pm\frac{1}{\sqrt{2}}\right) \end{equation*}

     et

     \begin{equation*} \left(\pm\frac{1}{\sqrt{2}},\pm\frac{1}{\sqrt{2}},0\right). \end{equation*}

   • Cas 3 : Deux coordonnées nulles.

     Commençons par le sous-cas où \(x=y=0\) et \(z\neq 0\text{.}\)

     Alors \((E_4)\) entraîne donne

     \begin{equation*} z^2=1. \end{equation*}

     Ce sous-cas conduit donc aux deux points suivants

     \begin{equation*} \left(0,0,\pm 1\right). \end{equation*}

     Et pour des raisons de symétrie, on ajoute aussi à ce cas les points

     \begin{equation*} \left(0,\pm 1,0\right) \end{equation*}

     et

     \begin{equation*} \left(\pm 1,0,0\right). \end{equation*}

2. On évalue maintenant \(f\) en chacun de ces points :

   \begin{equation*} \begin{array}{c|c} &x^4+y^4+z^4\\ \hline \text{Cas 1}&3\left(\pm\frac{1}{\sqrt{3}}\right)^4=\dfrac{1}{3}\\ \text{Cas 2}&2\left(\pm\frac{1}{\sqrt{2}}\right)^4=\dfrac{1}{2}\\ \text{Cas 3}&(\pm 1)^4=1\\ \end{array} \end{equation*}

3. Le maximum cherché vaut donc

   \begin{equation*} 1 \end{equation*}

   et le minimum

   \begin{equation*} \frac{1}{3}. \end{equation*}

1. Commençons par calculer les gradients de

   \begin{equation*} f(x,y,z)=3x-y-3z,\; g(x,y,z)=x+y-z\;\text{et}\; h(x,y,z)=x^2+2z^2. \end{equation*}

   Cela donne

   \begin{equation*} \nabla f=\begin{bmatrix}3\\-1\\-3\end{bmatrix},\quad\quad\nabla g=\begin{bmatrix}1\\1\\-1\end{bmatrix}\quad\text{et}\quad\nabla h=\begin{bmatrix}2x\\0\\4z\end{bmatrix}. \end{equation*}

   On doit donc résoudre le système

   \begin{equation*} \begin{cases}\nabla f=\lambda\nabla g+\mu\nabla h\\g(x,y,z)=0\\h(x,y,z)=1\end{cases} \end{equation*}

   qui donne les cinq équations suivantes

   \begin{alignat*}{2} (E_1)\quad && 3& {}={} \lambda+2\mu x\\ (E_2)\quad && -1& {}={} \lambda\\ (E_3)\quad && -3& {}={} -\lambda+4\mu z\\ (E_4)\quad &&x+y-z & {}={} 0\\ (E_5)\quad &&x^2+2z^2 & {}={} 1. \end{alignat*}

   En remplaçant \(\lambda\) par \(-1\text{,}\) grâce à \((E_2)\text{,}\) dans \((E_1)\) et \((E_3)\text{,}\) on obtient

   \begin{equation*} 4=2\mu x=-4\mu z \end{equation*}

   dont on déduit d'abord que \(\mu\neq 0\text{,}\) puis que

   \begin{equation*} 2x=-4z\quad\text{d'où}\quad x=-2z. \end{equation*}

   Alors \((E_4)\) entraîne

   \begin{equation*} y=z-x=z-(-2z)=3z. \end{equation*}

   Enfin \((E_5)\) donne

   \begin{equation*} (-2z)^2+2z^2=1\quad\text{d'où}\quad z^2=\frac{1}{6}\quad\text{et}\quad z=\pm\frac{1}{\sqrt{6}}. \end{equation*}

   On trouve donc deux points :

   \begin{equation*} \left(-\frac{2}{\sqrt{6}},\frac{3}{\sqrt{6}},\frac{1}{\sqrt{6}}\right) \end{equation*}

   et

   \begin{equation*} \left(\frac{2}{\sqrt{6}},-\frac{3}{\sqrt{6}},-\frac{1}{\sqrt{6}}\right). \end{equation*}

2. On évalue maintenant \(f(x,y,z)=3x-y-3z\) en chacun de ces deux points : on trouve

   \begin{equation*} \left(-\frac{2}{\sqrt{6}},\frac{3}{\sqrt{6}},\frac{1}{\sqrt{6}}\right)=3\left(-\frac{2}{\sqrt{6}}\right)-\frac{3}{\sqrt{6}}-3\frac{1}{\sqrt{6}}=-\frac{12}{\sqrt{6}} \end{equation*}

   et

   \begin{equation*} \left(\frac{2}{\sqrt{6}},-\frac{3}{\sqrt{6}},-\frac{1}{\sqrt{6}}\right)=3\frac{2}{\sqrt{6}}-\left(-\frac{3}{\sqrt{6}}\right)-3\left(-\frac{1}{\sqrt{6}}\right)=\frac{12}{\sqrt{6}}. \end{equation*}

3. Le maximum cherché vaut donc

   \begin{equation*} \frac{12}{\sqrt{6}}=2\sqrt{6} \end{equation*}

   et le minimum

   \begin{equation*} -\frac{12}{\sqrt{6}}=-2\sqrt{6}. \end{equation*}

Soit les fonctions

1. Commençons par la recherche des points critiques de \(f\) : on a

   \begin{align*} \nabla f=\vec{0}&\quad\Leftrightarrow\quad\begin{cases}4x-4=0\\6y=0\end{cases}\\ &\quad\Leftrightarrow\quad\begin{cases}x=1\\y=0\end{cases} \end{align*}

   et comme \(\nabla f\) existe partout, il n'y a pas d'autre point critique.

   Par ailleurs, le point \((1,0)\) vérifie

   \begin{equation*} g(1,0)=1^2+0^2=1<16 \end{equation*}

   donc on le retient pour l'étape 3.

2. Calculons les gradients de \(f\) et de \(g\)

   \begin{equation*} \nabla f=\begin{bmatrix}4x-4\\6y\end{bmatrix}\quad\text{et}\quad\nabla g=\begin{bmatrix}2x\\2y\end{bmatrix}. \end{equation*}

   On résout alors le système

   \begin{equation*} \begin{cases}\nabla f=\lambda\nabla g\\g(x,y)=16\end{cases} \end{equation*}

   qui donne les trois équations suivantes

   \begin{alignat*}{1} 4x-4 & {}={} 2\lambda x\\ 6y & {}={} 2\lambda y\\ x^2+y^2 & {}={} 16 \end{alignat*}

   soit

   \begin{alignat*}{2} (E_1)\quad&& 2x-2 & {}={} \lambda x\\ (E_2)\quad&& 3y & {}={} \lambda y\\ (E_3)\quad&&x^2+y^2 & {}={} 16 \end{alignat*}

   où \((E_2)\) est équivalente à

   \begin{equation*} (3-\lambda)y=0 \end{equation*}

   et conduit à l'alternative qui suit.

   • Cas \(\lambda=3\) : Alors \((E_1)\) devient

     \begin{equation*} 2x-2=3x\quad\text{d'où}\quad x=-2 \end{equation*}

     puis \((E_3)\) donne

     \begin{equation*} (-2)^2+y^2=16\quad\text{d'où}\quad y^2=12\quad\text{soit}\quad y=\pm 2\sqrt{3}. \end{equation*}

   • Cas \(y=0\) : Alors \((E_3)\) donne

     \begin{equation*} x^2=16\quad\text{soit}\quad x=\pm 4. \end{equation*}

   On retient donc les points

   \begin{equation*} (-2,\pm 2\sqrt{3})\quad\text{et}\quad (\pm 4,0) \end{equation*}

   pour l'étape 3.

3. Évaluons maintenant \(f\) aux points trouvés précédemment :

   \begin{equation*} \begin{array}{c|c} (x,y)&f(x,y)=2x^2+3y^2-4x-5\\ \hline (1,0)&2\cdot 1+3\cdot 0-4\cdot 1-5=-7\\ (-2,\pm 2\sqrt{3})&2\cdot 4+3\cdot 12-4\cdot(-2)-5=47\\ (-4,0)& 2\cdot 16+3\cdot 0-4\cdot(-4)-5=43\\ (4,0)& 2\cdot 16+3\cdot 0-4\cdot 4-5=11 \end{array} \end{equation*}

4. Le maximum cherché vaut donc

   \begin{equation*} 47 \end{equation*}

   et il est atteint aux points \((-2,\pm 2\sqrt{3})\text{.}\)

   Le minimum vaut quant à lui

   \begin{equation*} -7 \end{equation*}

   et il est atteint au point \((1,0)\text{.}\)